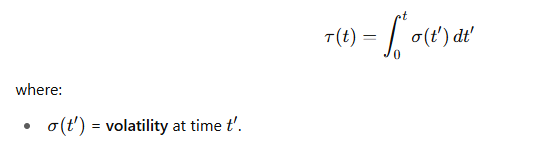私が18歳のとき、友人たちと釣りに出かけました。
その途中で、車のタイヤの1つが破裂しました。車は道路上で何度も横転し、最終的に側溝に落ちました。
幸運なことに、誰も怪我はしませんでした。
しかし、その後の会話の中で、私たちは皆、事故の瞬間が信じられないほど長く感じられたと覚えていました。外部の観察者にとっては、すべてが数秒以内に起こったにもかかわらずです。

この現象は、危機的または命に関わる状況を経験した人々によく語られます。
まるで時間そのものが遅く流れるかのように感じられるのです。

私たちは通常、時間を線形な次元として考えていますが、特殊相対性理論によれば、時間は非線形なのです。

では、この理解を外国為替取引にどのように応用できるのでしょうか？

外国為替取引における非線形時間

移動する物体の時計は静止している物体に比べて遅く進む（特殊相対性理論）

📘 科学的に言えば：
物体が高速で移動すると（特に光速に近い速度で）、

👉 物体の移動速度が速ければ速いほど、静止している観察者にとってその物体の時間の流れは遅くなります。

⏰ 直感的に言えば：
もしあなたが光速の99.999%で移動する宇宙船の中にいたら、
あなたにとって1時間が経過する間に、地球上では10年が経過するでしょう。

あなたは実質的に時間を「切り抜けて」移動しているのです。

📈 トレーディングの類推：

価格が急上昇する市場を想像してみてください。

• その瞬間、市場の時間は圧縮され、すべてが一瞬で起こります。
• ムーブメントの内部にいるトレーダーにとって、時間は「通常通り」に感じられます。
• 外部の観察者にとっては、それは突然の閃光のように見えます。

🔵 強力な市場インパルス = 相対性理論におけるロケット
🔵 ムーブメントの内部の時間は、外部と比較して遅く流れます。

巨大な物体の近くでは時間が遅くなる

（🌌 一般相対性理論）

📘 科学的に言えば：
重力はそれ自体が力ではなく、質量によって時空が曲がることです。
ブラックホールのような巨大な物体に近づくほど、時間の流れは遅くなります。

⏰ 直感的に言えば：

• 地球の軌道上では、地表よりも時間が速く進みます。
• ブラックホールの近くでは、時間がほとんど止まります。

外部の観察者から見ると、物体は事象の地平面で「停止」したように見えますが、内部では時間は通常に流れています。

📈 トレーディングの類推：
巨大な重力の影響 = 重要な市場イベント（例：NFP発表、FOMC会議、地政学的ショック）

市場がそのようなイベントに近づくと：

• 価格の動きが遅くなる（期待による）
• 取引量が減少（トレーダーが様子を見る）
• 市場時間が引き伸ばされ、現実が「一時停止」したかのように感じられる

そしてイベント後、市場時間は「爆発」し、動きが急激に加速します。

🧠 要約表 — 物理学 vs トレーディング：

物理学の概念	トレーディングの類推
🚀 高速運動	市場インパルス、ブレイクアウト、ニュースイベント
⌛ 時間の遅延	レンジ相場、蓄積、ニュース待ち
🌌 重力	主要プレイヤーやファンダメンタル要因の影響
📉 時間の歪み	ATR拡大、ボラティリティの急上昇、非線形市場時間

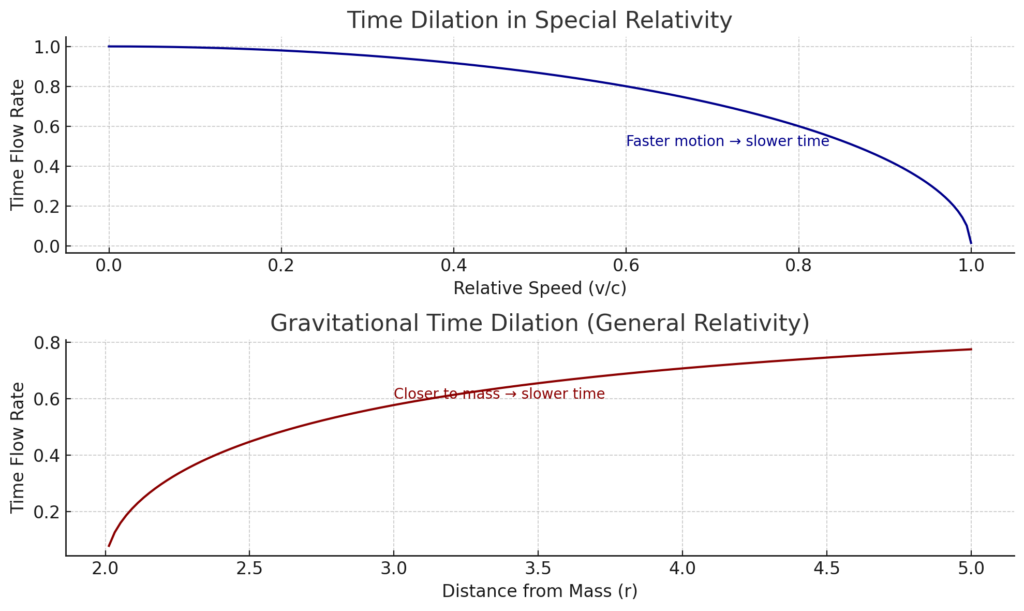
ここでは、物理学における時間の非線形な振る舞いと、それがトレーディングにどのように関連するかを視覚的に説明しています。

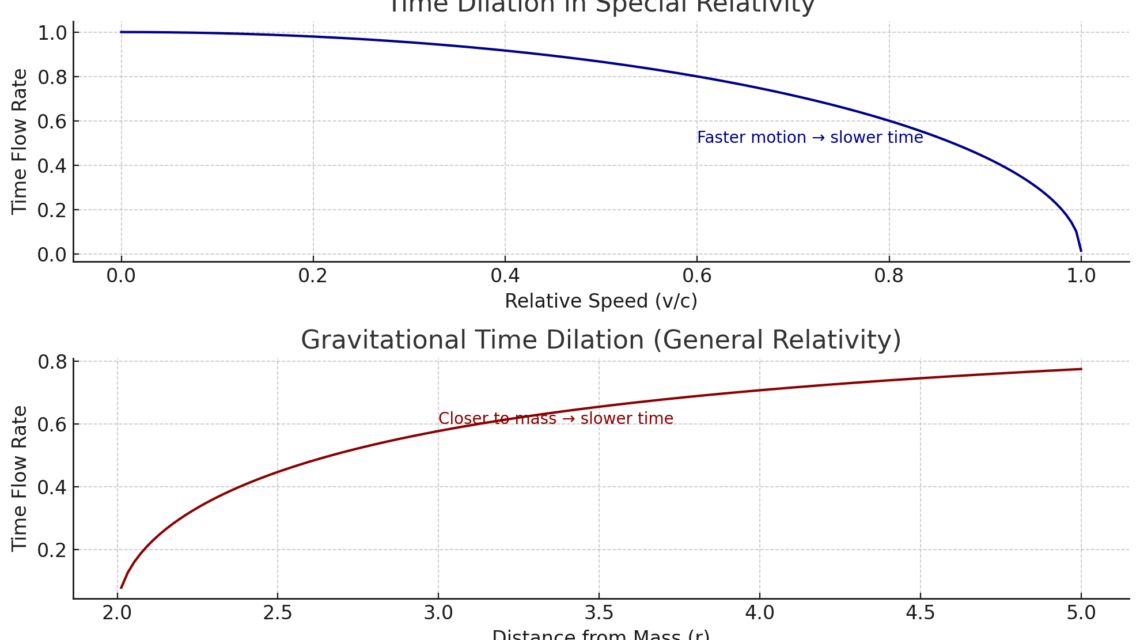
🔷 チャート1：特殊相対性理論 — 速度が時間を遅らせる

• 物体が速く動けば動くほど（光速に近づくほど）、静止している観察者に対して時間の流れは遅くなります。
• トレーディングで言えば：
  📈 高速市場ムーブメント（インパルス）において、内部の参加者にとって時間は圧縮され、すべてが速くスムーズに感じられます。

🔴 チャート2：一般相対性理論 — 重力が時間を遅らせる

• 物体が重力源に近づくほど、時空の曲がりによって時間の流れが遅くなります。
• トレーディングでは：
  🧲 主要経済イベント（NFP、FOMC、地政学リスク）は重力井戸のように機能します。
  市場が遅くなり、凍結し、圧力が高まり、時間が引き伸ばされるのです。

💡 外国為替取引における非線形時間の例

10分間のEUR/USDチャートを想像してください：

• 9分間は市場がフラット（価格はわずか3ピップス内で変動）
• 1分間だけニュースによる急激なボラティリティスパイクが発生し、30ピップス急騰

⏰ 線形時間の場合：

• 10分間すべてが等しく重要とみなされます。
• SMA、RSI、MACDのようなインディケーターは、すべての動きを単純に平均化します。

🌀 「市場時間」（非線形時間）では：

• フラットな9分間は圧縮され、ほぼゼロになります。
• 高ボラティリティの1分間は拡大し、「1日続いた」かのように伸びます。
• インディケーターはフラット期間では「遅く」なり、活動期には「加速」します。

📊 物理学の類推：

特殊相対性理論：

• 高速で移動する物体の時計は、静止している観察者と比べて遅く進みます。

一般相対性理論：

• 巨大な質量体の近くでは時間が引き伸ばされます（重力による時間の遅れ）。

トレーディングにおいて：

• フラットな市場は静止物体のように振る舞い → 時間が止まる。
• 価格インパルスは超空間ジャンプのよう → 時間が飛ぶ。

🔍 市場時間の公式：

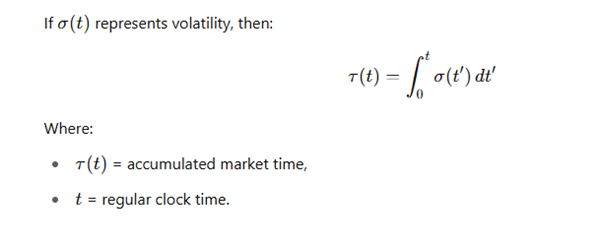
📏 数値例：

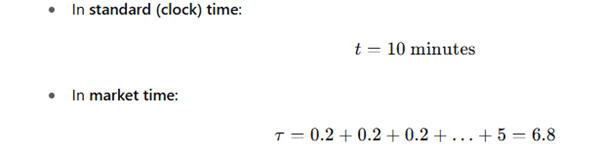
この1分間のボラティリティは、9分間の静寂よりもはるかに「重い」のです。

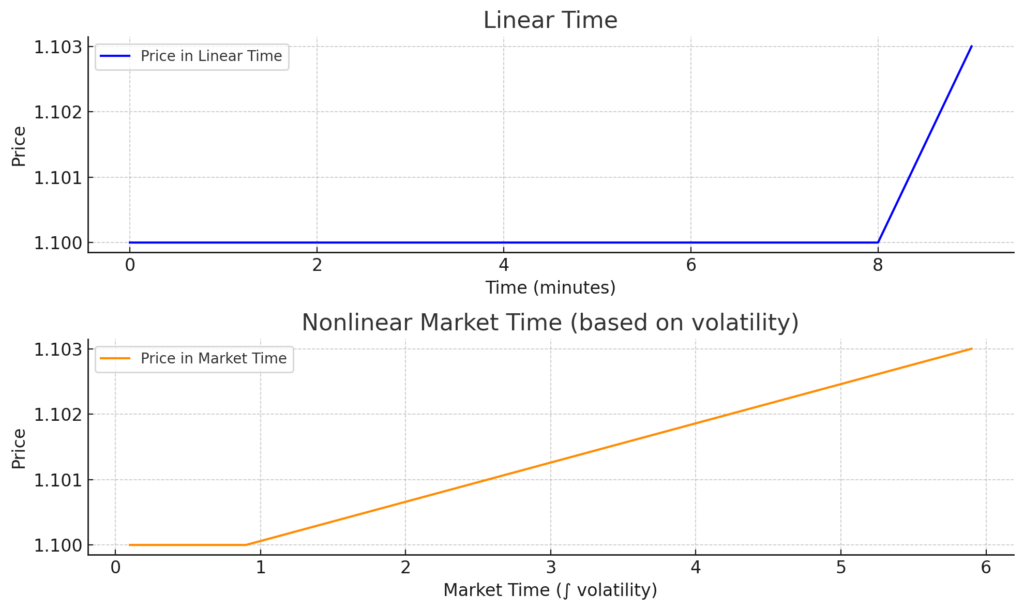
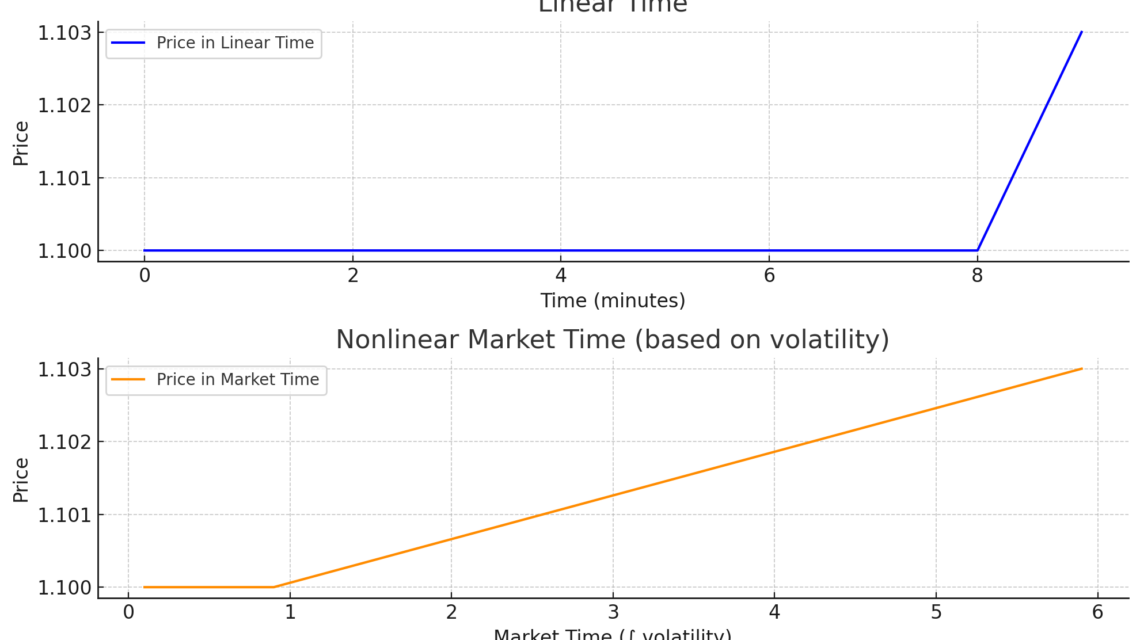
これはトレーディングにおける非線形時間の視覚的デモンストレーションです：

🔷 上のチャート：線形時間

• 各分が等しく扱われます。
• 9分間は価格がほぼフラットで、最後の1分間に急上昇します。

🟠 下のチャート：非線形市場時間

• ボラティリティ（市場活動）に基づいて時間が引き伸ばされます。
• 最後のボラティリティが高い1分間が拡大し、フラットな期間は圧縮されます。
• これは相対論的時間を模倣します：動きが多いほど体感時間も長くなります。

🧠 実際には、市場時間に基づいて設計されたインディケーターは：

• 意味のある変化に素早く反応します。
• 情報量の少ないフラットエリアを無視します。
• 高ボラティリティ時のトレーダーの「時間感覚」によりマッチします。

🔍 外国為替標準テクニカルインディケーターの問題点

RSI、MACD、移動平均などのインディケーターは：

• 線形かつ絶対的な時間を仮定しています。
• 固定スケール（バー1、バー2、バー3…）で動作します。
• 市場の「圧縮」や「拡張」に適応しません。

📌 実際には、市場は非線形時間に従っています：

• ある時は、5分間が1時間並みに重みを持ちます（高ボラティリティ）。
• またある時は、3日間が影のように過ぎ去ります（低ボラティリティ、レンジ市場）。

🚀 相対論的アプローチを適用したらどうでしょうか？

🔸 アイデア： 市場を時空構造として考えます。

• 価格 = 座標xxx、
• 時間 = ttt、
• しかし時間は絶対ではなく、市場相対的です。
• チャート上の各点 = 時空間におけるイベント。

🔬 どのようなテクニカルインディケーターを構築できるか？

🔧 相対論的RSI（RRSI）:

• 通常のRSIですが、非線形時間スケールで計算されます。
• ローソク足は「加速された」時間τ(t)で重み付けされます。
• 急激なボラティリティスパイクでは時間が伸び、RSIがより迅速に反応します。

🤯 さらに進んで：

🧭 時間の曲率指数（TCI）:

• 市場時間の曲がり具合とその方向を測定します。
  • 📈 正の曲率 → 加速（重力的引き寄せのような）、
  • 📉 負の曲率 → 減速または停滞。

⚙️ 実装アイデア：

• 通常のバーではなく、市場時間に基づく重み付き計算を使用。
• 時空間グリッドの変形としてビジュアル化。
• 機械学習を使って市場メトリック（ボラティリティ、出来高、ティック密度、ニュース反応など）をモデル化。

🚀 ボーナス：実際にボラティリティ積分を計算する方法

📘 相対性理論では：

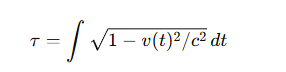
📈 市場では：

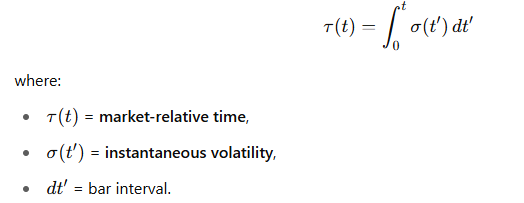
🛠 実用的な計算方法：

🔸 ステップ1: ボラティリティσ(t)を推定

オプション：

💠 絶対ボラティリティ:

sigma = abs(price[t] - price[t-1])

💠 移動標準偏差:

sigma = price_series.rolling(window).std()

💠 ATR（平均真幅）:

import ta
sigma = ta.volatility.AverageTrueRange(high, low, close, window=14).average_true_range()

🔸 ステップ2: 時間に対してボラティリティを積分

離散データでは、単純な累積和になります：

rel_time = np.cumsum(sigma.values)

これにより、rel_time[i]は、市場が「内部時間」でどれだけ進んだかを示します（単なるカレンダー時間ではなく）。

---

📊 シンプルなPython例：

import numpy as np
import pandas as pd

# 価格配列があると仮定
price = np.array([...])

# 絶対ボラティリティを計算
sigma = np.abs(np.diff(price, prepend=price[0]))

# ボラティリティを積分
rel_time = np.cumsum(sigma)

>>>Learn more about professional software for Arbitrage Trading – SharpTrader