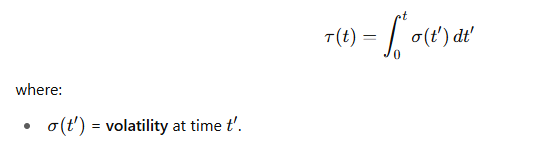내가 18살이었을 때, 몇몇 친구들과 낚시를 하러 갔다.
가는 길에 차의 타이어 중 하나가 터졌다. 차량은 도로 위에서 여러 번 구르다가 결국 도랑에 빠졌다.
우리는 운이 좋게도 아무도 다치지 않았다.
하지만 사고 직후 대화에서 우리는 모두 사고 순간이 믿을 수 없을 정도로 길게 느껴졌다고 기억했다. 외부 관찰자에게는 모든 일이 몇 초 만에 일어난 것처럼 보였을 텐데 말이다.

이 현상은 위급하거나 생명을 위협하는 상황을 겪은 사람들이 종종 묘사하는 것이다.
마치 시간 자체가 느려지는 것처럼 느껴진다.

우리는 보통 시간을 선형 차원으로 생각하지만, 특수 상대성 이론에 따르면 시간은 비선형적이다.

그렇다면 이 개념을 외환 거래에 어떻게 적용할 수 있을까?

외환 거래에서의 비선형 시간

움직이는 물체의 시계는 정지된 물체에 비해 느리게 간다 (특수 상대성 이론, STR)

📘 과학적으로:
어떤 물체가 고속으로 (특히 빛의 속도에 가깝게) 이동하면:

👉 물체가 빨리 움직일수록, 정지된 관찰자에 비해 그 물체의 시간은 더 느리게 흐른다.

⏰ 직관적으로:
만약 당신이 빛의 속도의 99.999%로 이동하는 우주선 안에 있다면,
당신에게는 한 시간이 흐르지만,
지구에서는 10년이 흐른다.

즉, 당신은 시간 자체를 “가로질러 이동”하는 것이다.

📈 거래 비유:

가격이 엄청난 속도로 상승하는 시장을 상상해보자.

• 그 순간, 시장 시간은 압축된다 — 모든 것이 매우 빠르게 일어난다.
• 그 움직임 안에 있는 트레이더들에게는 시간이 “정상적”으로 느껴진다.
• 외부 관찰자에게는 번쩍이는 순간처럼 보인다.

🔵 강력한 시장 충격 = 상대성 이론의 로켓.
🔵 움직임 안에서는 시간이 느려지고, 외부에 비해 다르게 흐른다.

거대한 물체 근처에서는 시간이 느려진다

(🌌 일반 상대성 이론, GTR)

📘 과학적으로:
중력은 본질적으로 힘이 아니라, 질량이 시공간을 구부리는 것이다.
블랙홀 같은 거대한 물체에 가까워질수록, 당신에게 시간은 더 느리게 흐른다.

⏰ 직관적으로:

• 지구 궤도에서는 지표면보다 시간이 더 빨리 흐른다.
• 블랙홀 근처에서는 시간이 거의 멈춘다.

외부 관찰자가 보기에는, 물체가 사건의 지평선에 “얼어붙는” 것처럼 보인다. 하지만 내부에서는 시간이 정상적으로 흐른다.

📈 거래 비유:
거대한 중력체 = 주요 시장 이벤트 (예: NFP 발표, FOMC 회의, 지정학적 충격).

시장이 이런 이벤트에 접근할 때:

• 가격 움직임이 느려진다 (기대감),
• 거래량이 감소한다 (트레이더들이 멈춘다),
• 시장 시간이 늘어나 현실이 “멈춘” 것처럼 느껴진다.

그리고 이벤트 이후 — 시장 시간은 “폭발”하고 가격은 급격히 움직인다.

🧠 요약 표 — 물리학 vs 거래:

물리학 개념	거래 비유
🚀 빠른 운동	시장 충격, 돌파, 뉴스 이벤트
⌛ 시간 지연 (느려짐)	박스권, 매집, 뉴스 대기
🌌 중력	주요 플레이어나 펀더멘털 요인의 영향
📉 시간 왜곡	ATR 확장, 변동성 급등, 비선형 시장 시간

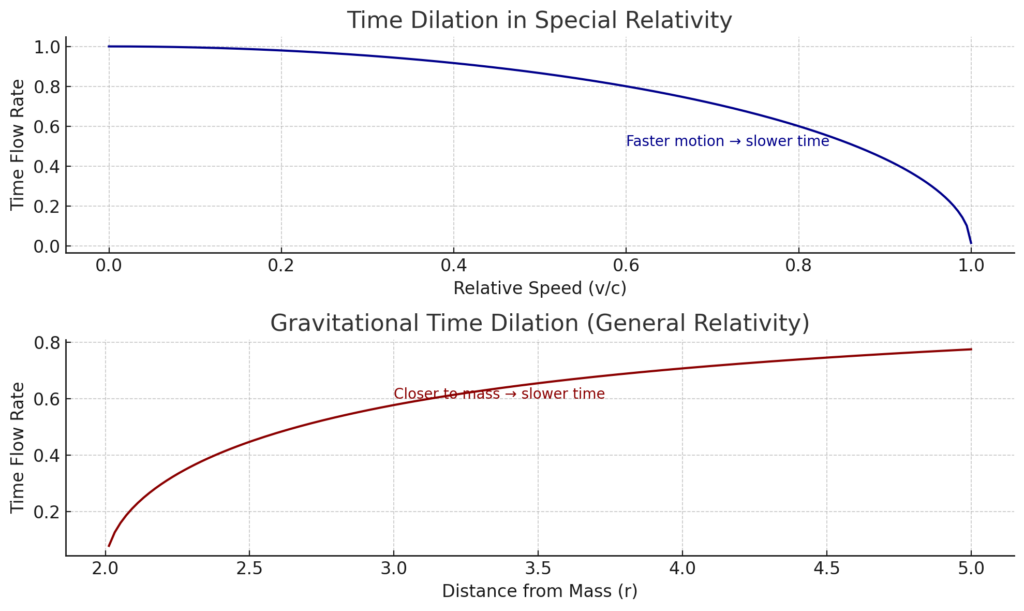
다음은 물리학에서 시간 비선형성이 어떻게 작용하는지, 그리고 그것이 거래와 어떻게 관련되는지를 보여주는 시각적 설명입니다.

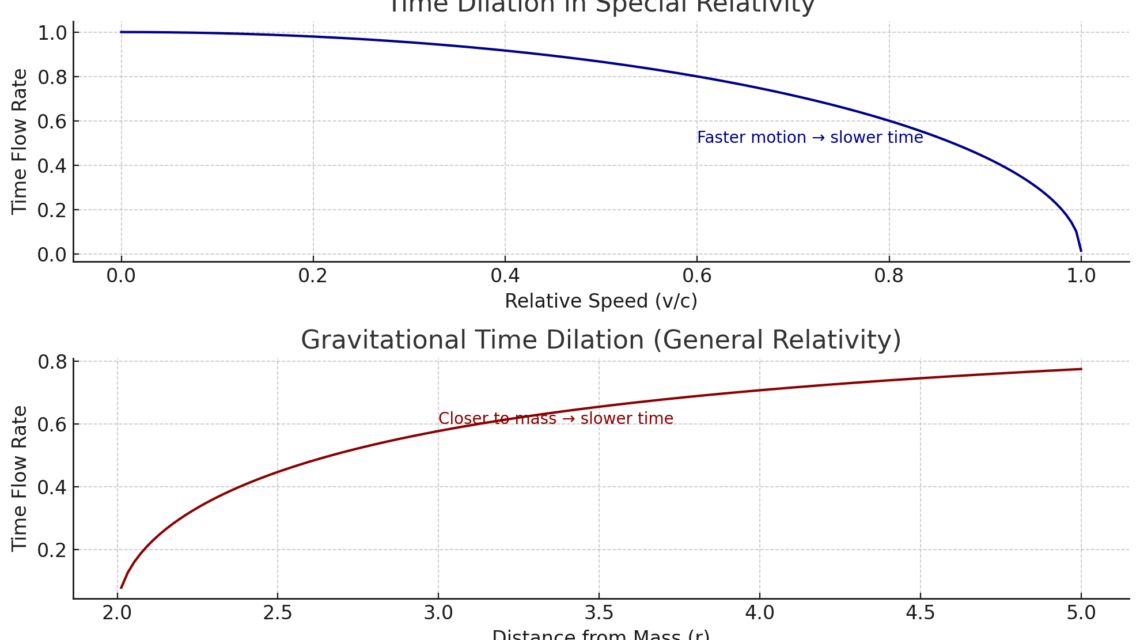
🔷 차트 1: 특수 상대성 이론 — 속도가 시간을 늦춘다

• 물체가 빠르게 움직일수록 (빛의 속도에 가까울수록), 시간 흐름이 느려진다 (정지된 관찰자에 비해).
• 거래 용어로는:
  📈 고속 시장 움직임 (충격)은 내부 참가자에게 시간 압축을 가져온다 — 모든 것이 빠르지만 부드럽게 느껴진다.

🔴 차트 2: 일반 상대성 이론 — 중력이 시간을 늦춘다

• 물체가 중력 질량에 가까워질수록, 시공간 곡률로 인해 시간이 느려진다.
• 거래에서는:
  🧲 주요 경제 이벤트 (NFP, FOMC, 지정학적 리스크)가 중력 우물처럼 작용한다.
  시장은 느려지고, 얼어붙고, 압력을 쌓는다 — 변동성이 줄어들면서 시간은 늘어난다.

💡 외환 거래에서 비선형 시간의 예

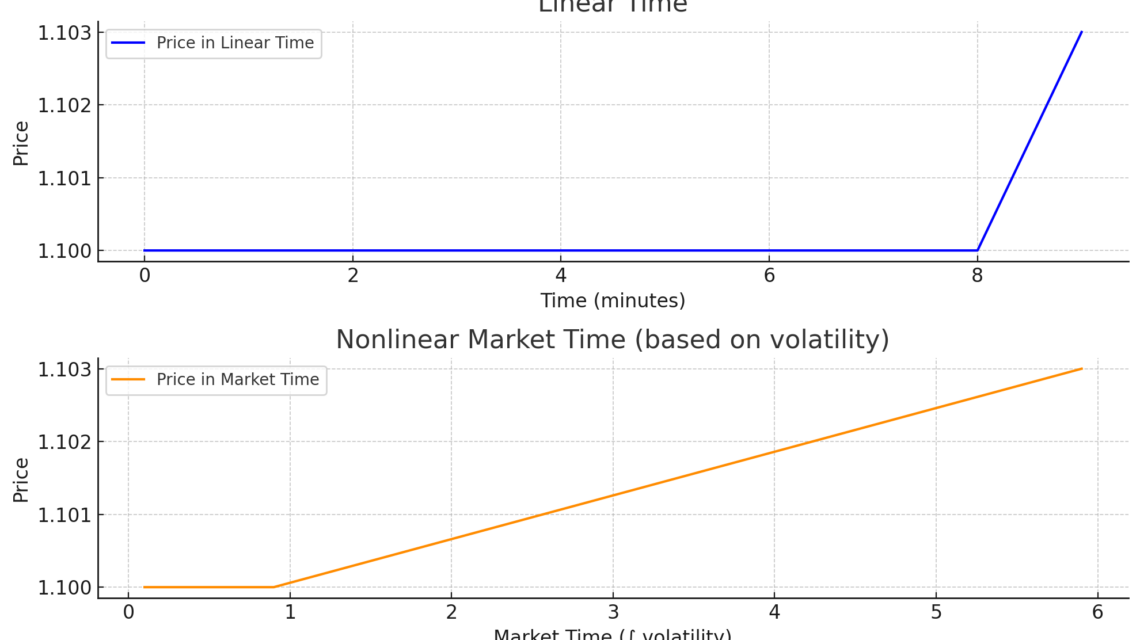
10분 동안의 EUR/USD 차트를 상상해보세요:

• 9분 동안 시장은 평평하게 유지되고 (가격 변동폭이 3핍 내외),
• 1분 동안 뉴스로 인한 변동성 급등이 발생하여 가격이 30핍 급등합니다.

⏰ 선형 시간에서는:

• 모든 10분이 동일한 중요성으로 간주됩니다.
• SMA, RSI, MACD 같은 지표들은 단순 평균만 할 뿐, 실제 영향을 인식하지 못합니다.

🌀 “시장 시간” (비선형 시간)에서는:

• 9분간의 평탄한 활동은 압축되어 거의 0에 가깝게 줄어듭니다.
• 1분간의 고변동성은 확장되어 하루 종일 지속된 것처럼 느껴집니다.
• 지표들은 평탄한 동안 느려지고, 활동 급등 시 가속됩니다.

📊 물리적 비유:

특수 상대성 이론:

• 빠르게 움직이는 물체의 시계는 정지된 관찰자에 비해 더 느리게 간다.

일반 상대성 이론:

• 거대한 질량체 근처에서는 시간이 느려진다 (중력 시간 지연).

거래에서는:

• 플랫 마켓은 정지된 물체처럼 행동 → 시간이 멈춘 듯하다.
• 가격 충격은 초공간 도약처럼 → 시간이 날아간다.

🔍 시장 시간 공식:

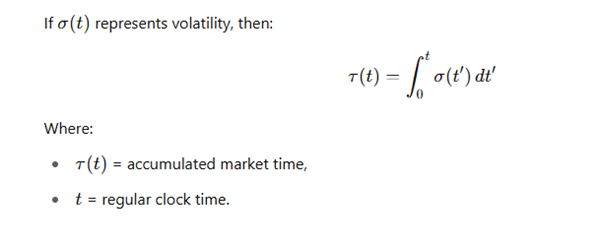
📏 숫자 예시:

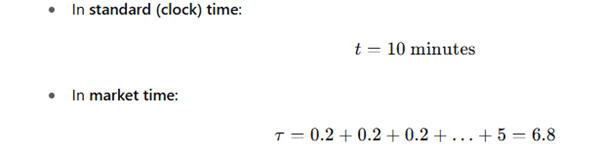
이 1분간의 높은 변동성은 9분간의 평온보다 훨씬 더 많은 “무게”를 지닙니다.

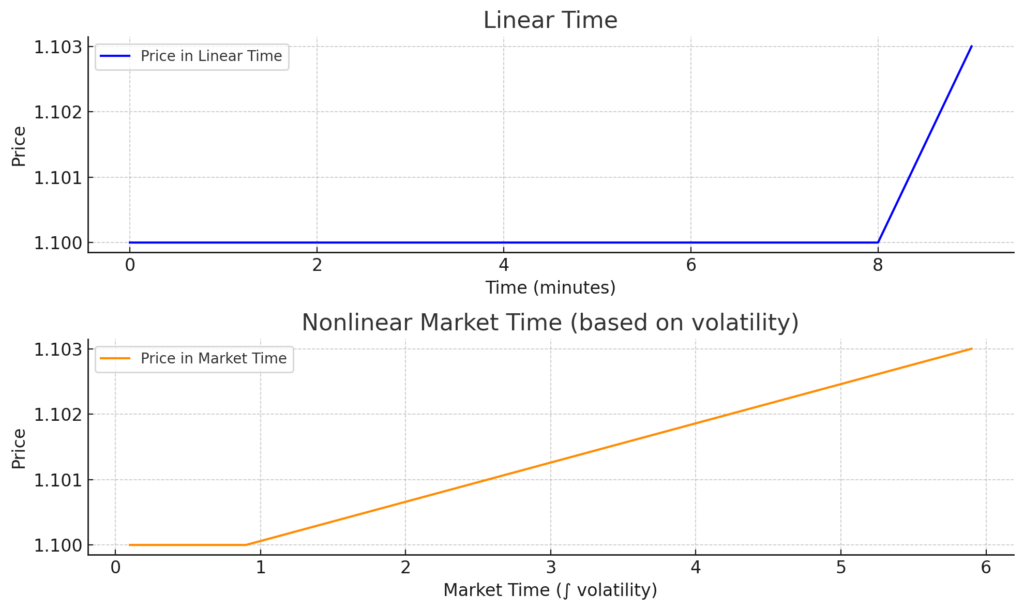
다음은 거래에서 비선형 시간을 시각적으로 나타낸 것입니다:

🔷 위 차트: 선형 시간

• 모든 분이 동일하게 처리됩니다.
• 9분 동안 가격이 거의 변하지 않다가 마지막 1분 동안 급등합니다.

🟠 아래 차트: 비선형 시장 시간

• 변동성에 따라 시간이 늘어나거나 압축됩니다.
• 마지막 1분간의 고변동성은 확장되고, 평탄한 시간은 압축됩니다.
• 이는 상대론적 시간을 모방합니다: 더 많은 움직임 = 더 많은 “체감 시간”.

🧠 실전에서는, 시장 시간에 기반한 지표들은:

• 의미 있는 변화에 더 빠르게 반응합니다.
• 정보가 적은 평탄한 구간을 무시합니다.
• 높은 변동성 순간에서 트레이더들이 느끼는 시간 감각과 더 잘 일치합니다.

🔍 외환 표준 기술 지표의 문제점

RSI, MACD, 이동 평균선 같은 지표들은:

• 선형적이고 절대적인 시간을 가정합니다.
• 고정된 스케일 (바 1, 바 2, 바 3…)에 따라 작동합니다.
• 시장 “압축”이나 “확장”에 적응하지 않습니다.

📌 실제로 시장은 비선형 시간을 따릅니다:

• 때때로, 5분이 1시간만큼 중요한 의미를 지닙니다 (고변동성),
• 다른 때는, 3일이 그림자처럼 스쳐갑니다 (낮은 변동성, 플랫).

🚀 그렇다면 상대론적 접근을 적용하면 어떨까요?

🔸 아이디어: 시장을 시공간 구조로 생각합니다:

• 가격 = 좌표 xxx,
• 시간 = ttt,
• 하지만 시간은 절대적이지 않고 시장 상대적입니다.
• 차트상의 각 점은 시공간 사건입니다.

🔬 어떤 외환 기술 지표를 만들 수 있을까?

🔧 상대론적 RSI (RRSI):

• 일반적인 RSI이지만 비선형 시간 스케일로 계산됩니다.
• 캔들은 “가속된 시간” τ(t)로 가중치가 부여됩니다.
• 급격한 변동성 확장은 RSI가 더 빠르게 반응하도록 합니다.

🤯 또는:

🧭 시간 곡률 지수 (TCI):

• 시장 시간이 얼마나 강하게, 어느 방향으로 굽어 있는지를 측정합니다:
  • 📈 양의 곡률 → 가속 (중력 인력과 유사),
  • 📉 음의 곡률 → 감속 또는 정체.

⚙️ 구현 아이디어:

• 일반적인 바(bar) 대신 시장 시간 가중치 ω를 기반으로 지표를 재계산합니다.
• 시공간 그리드 왜곡처럼 시각화합니다 (일반 상대성 이론의 그래프처럼).
• 기계 학습을 사용하여 변동성, 거래량, 틱 밀도, 뉴스 반응 등을 통해 시장 메트릭을 모델링합니다.

🚀 보너스: 변동성 적분을 실전에서 계산하는 방법

📘 상대성 이론에서는:

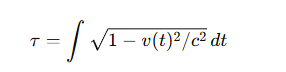
📈 시장에서는:

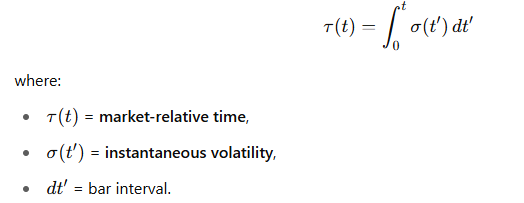
🛠 실제 계산 방법:

🔸 1단계: 변동성 σ(t) 추정

옵션:

💠 절대 변동성:

sigma = abs(price[t] - price[t-1])

💠 이동 표준 편차:

sigma = price_series.rolling(window).std()

💠 ATR (평균 진폭 범위):

import ta
sigma = ta.volatility.AverageTrueRange(high, low, close, window=14).average_true_range()

🔸 2단계: 시간에 따라 변동성 적분

이산 데이터에서는 단순 누적 합계입니다:

rel_time = np.cumsum(sigma.values)

따라서, rel_time[i]는 시장이 내부 시간에서 얼마나 “이동했는지”를 보여줍니다.

---

📊 간단한 Python 예시:

import numpy as np
import pandas as pd

# 가격 배열 가정
price = np.array([...])

# 절대 변동성 계산
sigma = np.abs(np.diff(price, prepend=price[0]))

# 변동성 적분
rel_time = np.cumsum(sigma)

>>>Learn more about professional software for Arbitrage Trading – SharpTrader