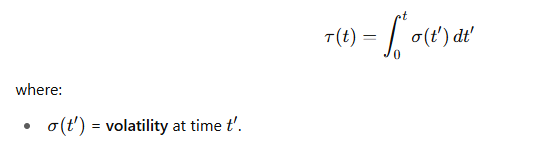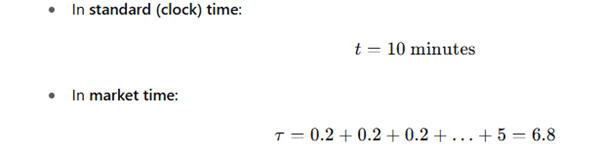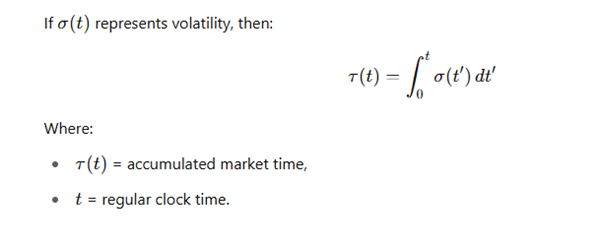Als ich 18 Jahre alt war, ging ich mit ein paar Freunden angeln.
Auf dem Weg platzte ein Reifen unseres Autos. Das Fahrzeug überschlug sich mehrmals auf der Straße und landete schließlich in einem Graben. Wir hatten Glück – keiner von uns wurde verletzt.
In den Gesprächen danach erinnerten wir uns jedoch alle daran, dass sich der Moment des Unfalls für uns unglaublich lang anfühlte, obwohl für jeden Außenstehenden alles innerhalb weniger Sekunden geschah.

Dieses Phänomen wird oft von Menschen beschrieben, die kritische oder lebensbedrohliche Situationen erleben.
Es fühlt sich an, als würde sich die Zeit selbst verlangsamen.

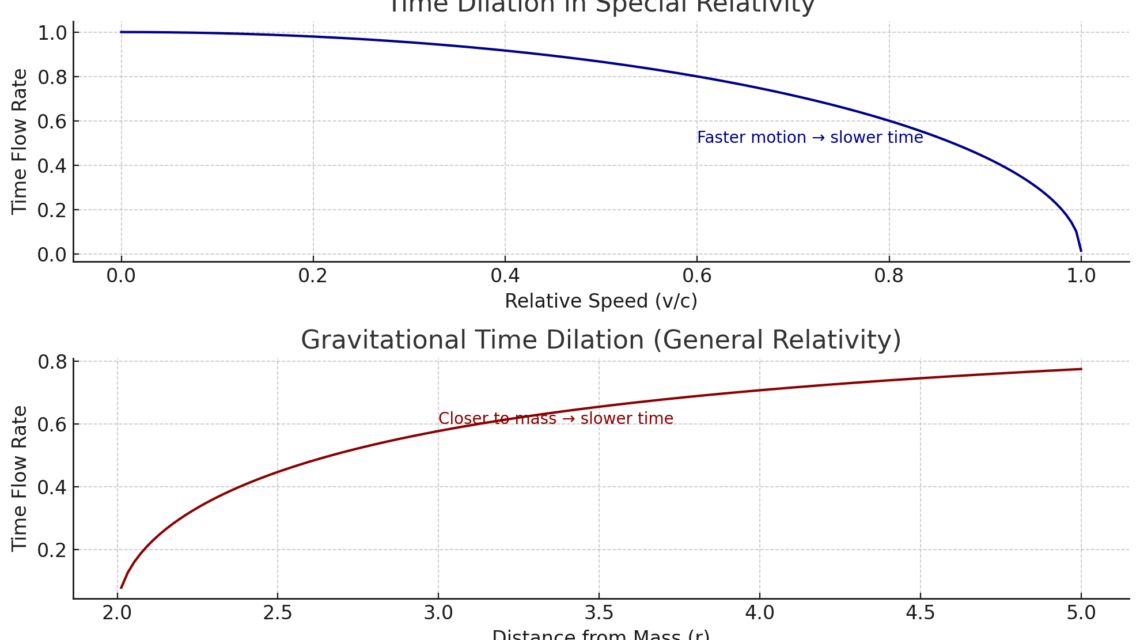
Wir sind es gewohnt, Zeit als eine lineare Dimension zu betrachten, aber laut der Spezialrelativitätstheorie ist die Zeit nichtlinear.

Die Frage ist also: Wie können wir dieses Verständnis auf den Forex-Handel anwenden?

Nichtlineare Zeit im Forex-Handel

Uhren in bewegten Objekten ticken langsamer relativ zu stationären Objekten (Spezialrelativitätstheorie, SRT)

…

🔍 Das Problem mit den Standard-Forex-Indikatoren

Indikatoren wie RSI, MACD und Gleitende Durchschnitte:

• gehen von einer linearen und absoluten Zeit aus,
• arbeiten auf einer festen Skala (Balken 1, Balken 2, Balken 3…),
• passen sich nicht an „Kompressionen“ oder „Expansionen“ des Marktes an.

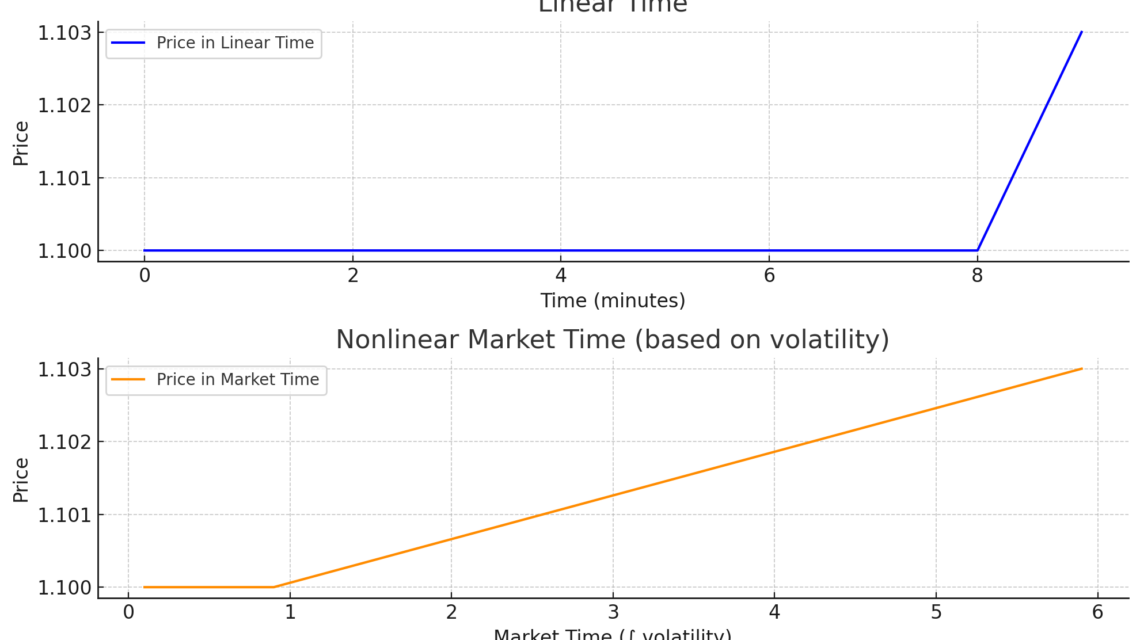
📌 In Wirklichkeit lebt der Markt nach nichtlinearer Zeit:

• Manchmal „wiegen“ 5 Minuten so viel wie eine Stunde (bei hoher Volatilität),
• Andere Male vergehen 3 Tage wie ein Schatten (bei geringer Volatilität und flachem Markt).

🚀 Was wäre, wenn wir einen relativistischen Ansatz anwenden würden?

🔸 Die Idee: Den Markt als Raumzeitstruktur betrachten, bei der:

• Preis = Koordinate xxx,
• Zeit = ttt,
• Aber Zeit ist nicht absolut — sie ist marktrelativ.
• Jeder Punkt auf einem Chart = ein Ereignis in der Raumzeit.

🔬 Welche Art von Forex-Indikator könnten wir bauen?

🔧 Relativistischer RSI (RRSI):

• Ein normaler RSI, aber berechnet auf einer nichtlinearen Zeitskala.
• Kerzen werden nach „beschleunigter“ Zeit τ(t) gewichtet.
• Plötzliche Volatilitätsspitzen dehnen die Zeit – der RSI reagiert schneller.

🤯 Oder sogar:

🧭 Zeitkrümmungsindex (TCI):

• Misst, wie stark und in welche Richtung sich die Marktzeit krümmt:
  • 📈 Positive Krümmung → Beschleunigung der Bewegung,
  • 📉 Negative Krümmung → Verlangsamung oder Stagnation.

⚙️ Umsetzungsideen:

• Indikatoren auf Basis der gewichteten Marktzeit ω neu berechnen, statt auf normalen Balken.
• Visualisierung als verzerrtes Gitter, ähnlich Raumzeitgrafiken in der allgemeinen Relativitätstheorie.
• Maschinelles Lernen verwenden, um die Marktmetrik zu modellieren (durch Volatilität, Volumen, Tick-Dichte, Nachrichtenreaktion etc.).

🚀 Bonus: Wie man das Volatilitätsintegral in der Praxis berechnet

📘 In der Relativitätstheorie:

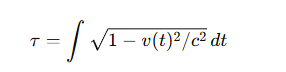
📈 Auf dem Markt:

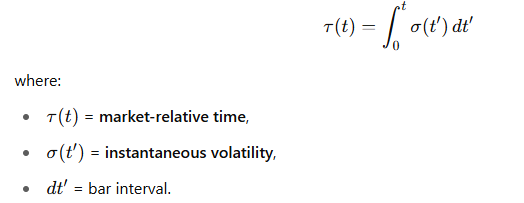
🛠 Praktische Berechnung:

🔸 Schritt 1: Volatilität schätzen σ(t)

Optionen:

💠 Absolute Volatilität:

sigma = abs(price[t] - price[t-1])

💠 Rollende Standardabweichung:

sigma = price_series.rolling(window).std()

💠 ATR (Durchschnittliche wahre Spanne):

import ta
sigma = ta.volatility.AverageTrueRange(high, low, close, window=14).average_true_range()

🔸 Schritt 2: Volatilität über die Zeit integrieren

rel_time = np.cumsum(sigma.values)

Damit zeigt rel_time[i] an, wie weit der Markt in seiner internen Zeit „gereist“ ist, nicht nur in Kalenderzeit.

📊 Einfaches Python-Beispiel:

import numpy as np
import pandas as pd

# Angenommen, wir haben ein Preis-Array
price = np.array([...])

# Berechne absolute Volatilität
sigma = np.abs(np.diff(price, prepend=price[0]))

# Integriere die Volatilität
rel_time = np.cumsum(sigma)

>>>Learn more about professional software for Arbitrage Trading – SharpTrader